1. PRODUCTO (MULTIPLICACIÓN) DE FRACCIONES ALGEBRAICAS
El
producto de fracciones algebraicas se obtiene multiplicando los numeradores
para luego dividir el resultado entre el producto de los denominadores.
Ejemplo:
P r
o c e d i m i e n t o
1. Se
factorizan las expresiones en los numeradores y denominadores
2. Se
simplifica, cancelando los factores comunes en numeradores y denominadores
3. Se
multiplican entre sí las expresiones ubicadas en los numeradores, el resultado
será el numerador de la fracción producto; asimismo, se multiplican entre sí
las expresiones escritas en los denominadores, este producto será el
denominador de la fracción resultado.
Consejo: Para
realizar los ejercicios siguientes es indispensable dominar por completo la
factorización, por lo cual recomiendo que se estudie primero, concienzudamente,
los casos de factorización.

Multiplicar

Anotamos
la multiplicación de los numeradores y de los denominadores:
Para dividir fracciones algebraicas procederemos igual como lo hacemos con fracciones, haciendo el producto cruzado de numeradores y denominadores, aunque antes de multiplicar debemos simplificar, si se puede.
Para
efectuar la división de fracciones se procede de la siguiente forma:
1. Se
invierte el divisor (el numerador se coloca en el denominador y, viceversa, el
denominador se ubica en el numerador) y, se procede a multiplicar el dividendo
por este divisor invertido
2. Las
fracciones se multiplican siguiendo los pasos siguientes:
a) Se
factorizan las expresiones
b) Se
simplifica, suprimiendo los factores comunes en los numeradores y denominadores.
c) Se
multiplican entre sí las expresiones que quedan en los numeradores; lo
propio se hace con las expresiones
que quedan en los denominadores; luego, para el
resultado, se ubica en el numerador el producto de los numeradores y
en el denominador el producto de los denominadores
Veamos ahora ejemplos de división (cociente) de fracciones
algebraicas
División
de expresiones mixtas
1.
Se
reducen a fracciones y se dividen como tales.
2.
Se
invierte el divisor (el numerador se coloca en el denominador y, viceversa, el
denominador se ubica en el numerador) y, se procede a multiplicar el dividendo
por este divisor invertido
3.
Las
fracciones se multiplican siguiendo los pasos siguientes.
a. Se factorizan las expresiones.
b. Se simplifica, suprimiendo los
factores comunes en los numeradores
y denominadores.
c. Se multiplican entre sí las
expresiones que quedan en los numeradores;
lo propio se hace con las
expresiones que quedan en los denominadores; luego, para el resultado, se ubica en el
numerador el producto de los numeradores y en el denominador el producto de los
denominadores.






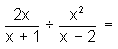




 (reduciendo a fracciones)
(reduciendo a fracciones)



 (efectuando el producto indicado)
(efectuando el producto indicado)















